Understand Activation Functions With A Real-World Analogy! #34
Neural Networks Building Blocks Simplified!
Hello Everyone,
Welcome to the 34th edition of my newsletter ML & AI Cupcakes!
In this newsletter, we will learn about activation functions which is one of the building blocks of neural networks. We will try to understand it with the help of a real-world analogy. After that, we’ll have a quick look at the commonly used activation functions.
Before, we move ahead, make sure you are familiar with other fundamental components like neurons, layers, weights and biases etc. of neural networks. Just in case you need, I have covered them up in the following links:
They have also been explained with real-life analogies…:)
What is an activation function?
In neural networks, the main role of an activation function is
to decide whether a neuron should be activated or not
how strong the signal of information should be
introducing non-linearity in the model
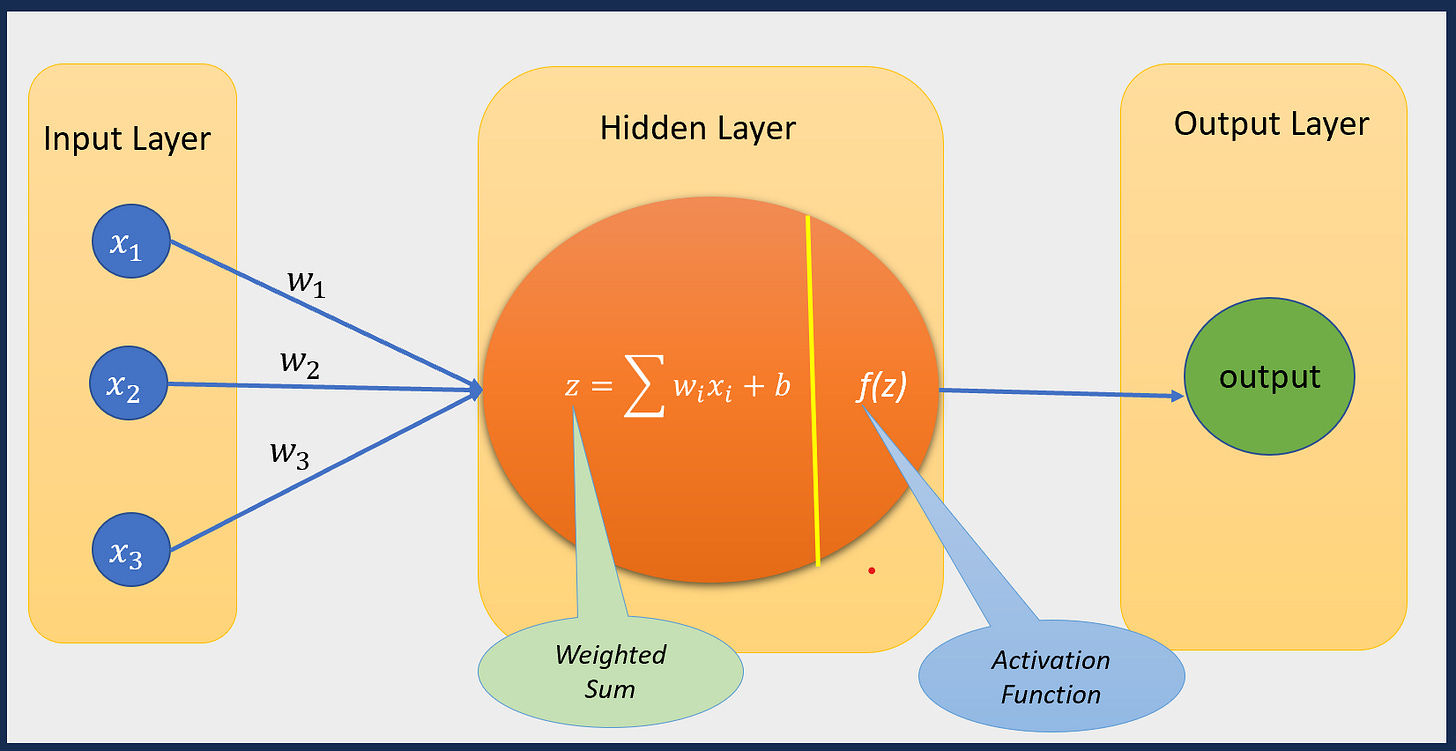
Each neuron receives inputs from the previous layer, apply some weights to calculate the weighted sum and then decides whether the information should be passed to the next layer or not.
Basically, a two-step sequential process happens in each neuron:
Step 1. Calculating the linear weighted sum
Step 2. Applying activation function on this linear weighted sum
Based on the results of step 2, it is decided whether a neuron should be activated or not.
If a neuron gets activated, its information will be passed to the next layer.
Otherwise, its information will not be passed.
In the following diagram, I have taken the example of the simplest neural network to make it easier for you to understand the above mentioned process. There is only one hidden layer with only one neuron.
Image credits: Author (Me)
Explaination with a real-world analogy
Let’s learn the concept of an activation function from a water tap knob.
Consider following similarities:
water pressure = input signal (weighted sum of neurons from previous layer)
water tap knob = activation function
water flow = output or information flow
Water tap knob controls the flow of water from the tap.
Now, whether the water will flow out of the tap or not, depends upon if we are turning the knob or not.
Also, even if we are turning the knob, how much water flows through the tap, depends upon how much we are truning the knob.
For example, if you turn it slightly, only a trickle will flow. If you turn it more, more water will start flowing. Turning of tap knob decides the amount of water that will flow through the tap.
Can you see its similarity with an activation function?
Activation function decides whether the information will be passed or not.
If the information is passed, how strong the signal is.
Why activation functions matter?
They act like gatekeepers. If they are not there, all the neurons will behave the same way and there will be no capturing or learning of complex non-linear patterns.
Without activation functions, it’s just like a linear regression from one layer to another. Because weighted sum is nothing but the same formula used for linear regression. It’s the activation function that adds more complexity or advancement to it.
Commonly used activation functions
There are different types of activation functions available. Choose them carefully based on your data complexities and prediction goals. Thier choice significantly influence the performance of a neural network.
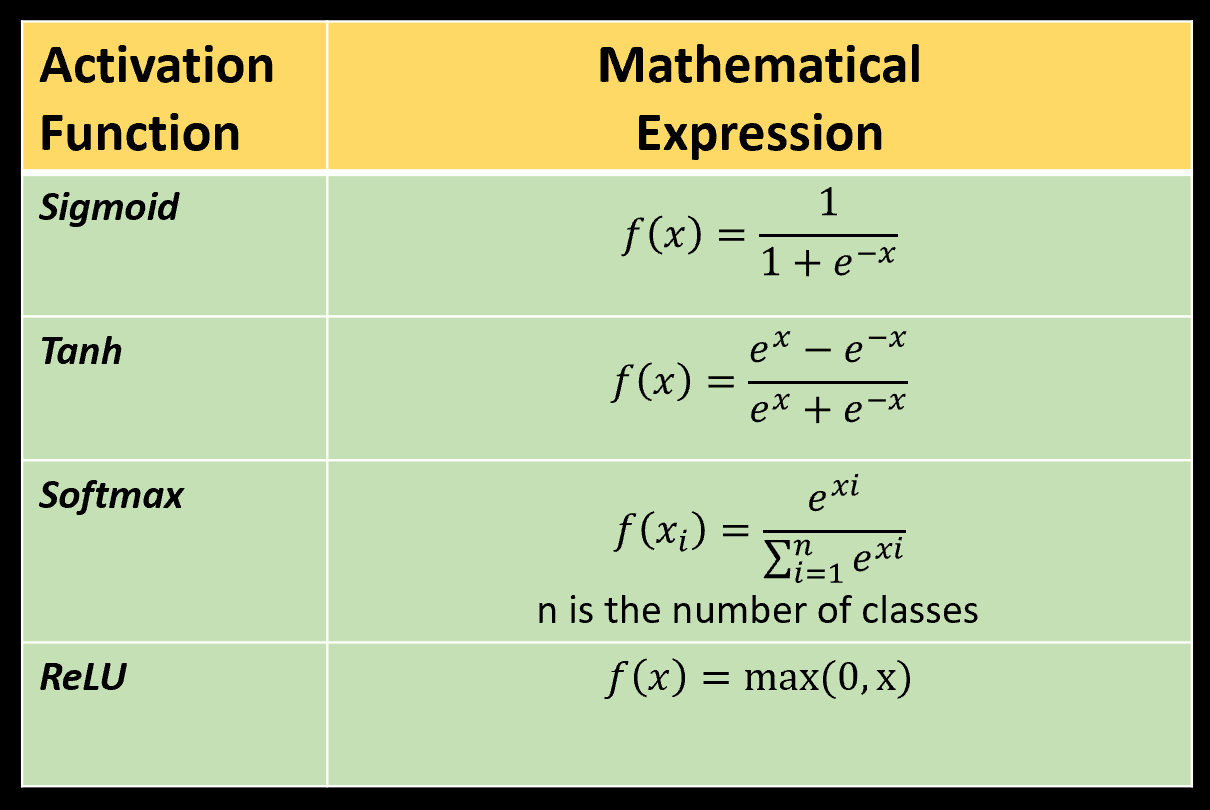
Some of the commonly used activation functions are provided in the table below:
Image Credit: Author (Me)
Sigmoid
It takes real values as input and transforms them into the range of [0,1]. It is useful for the problems where the objective is to predict probability. For example, binary classification problems. But it suffers from vanishing gradient problem.
tanh
It is similar to the sigmoid function. Though it provides the output between in the range of [-1,1].
Softmax
It is also an extension of sigmoid function. It is used in case of muti-class classification problems.
ReLU
It stands for Rectified Linear Unit. It is the most commonly used activation function in hidden layers of a neural network. It resolves the vanishing gradient problem occur in the sigmoid function. It takes real values as input and provides non-negative real values as output.
We’ll discuss about them in more detail in the upcoming newsletters!
Stay tuned for the same!
Writing each newsletter takes a lot of research, time and effort. Just want to make sure it reaches maximum people to help them grow in their AI/ML journey.
It would be great if you could share this newsletter with your network. Also, please let me know your feedbacks and suggestions in the comments section. That will help me keep going. Even a “like” on my posts will tell me that my posts are helpful to you.
See you soon!
-Kavita


Thanks!